GSP Juelich

So, I was selected for the GSP in Juelich, therefore I'll be in Juelich for 2 months and enjoying all the benefits of the JSC (including their clusters, e.g. Juwels, Jureca, ...). The first two weeks were dedicated to intensive courses about GPU Programming with CUDA, OpenACC and HIP. In the second week the course covered MPI and OpenMP. On the last day (today), we parallelized a n-body-simulation, which looks like this:

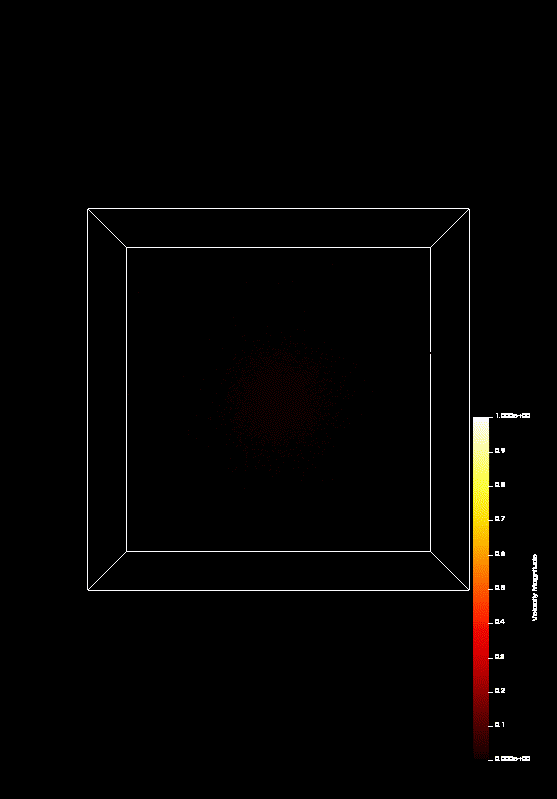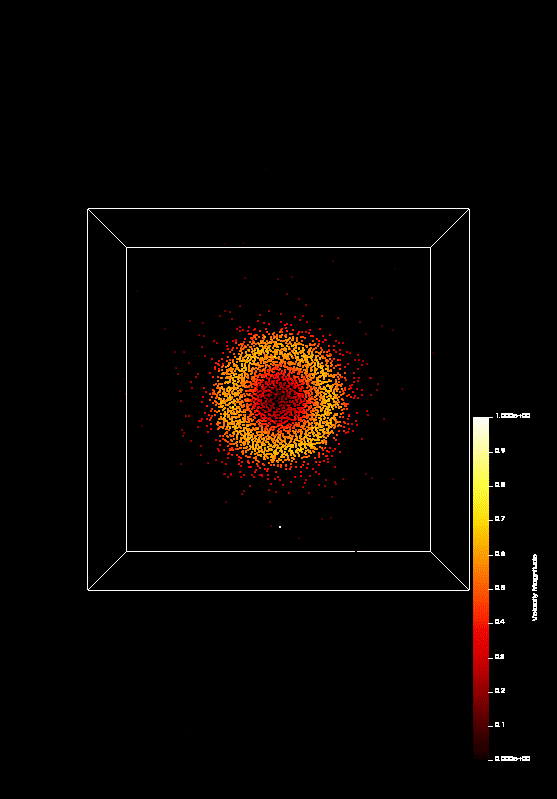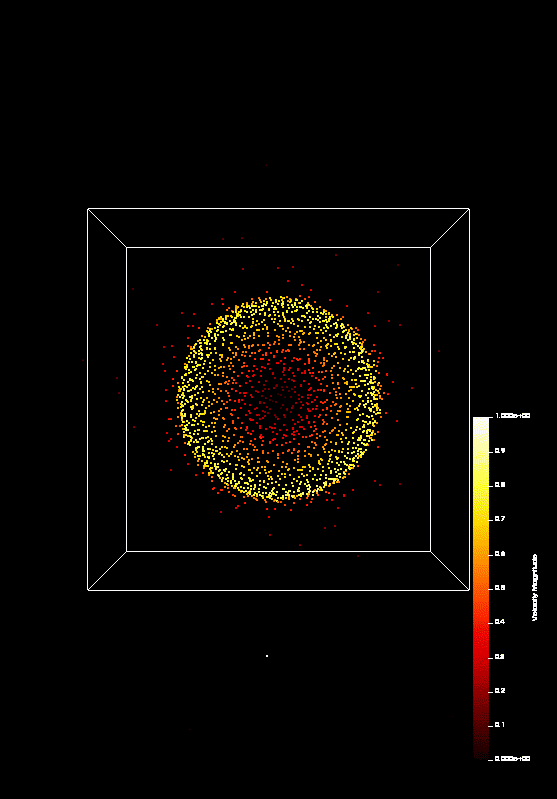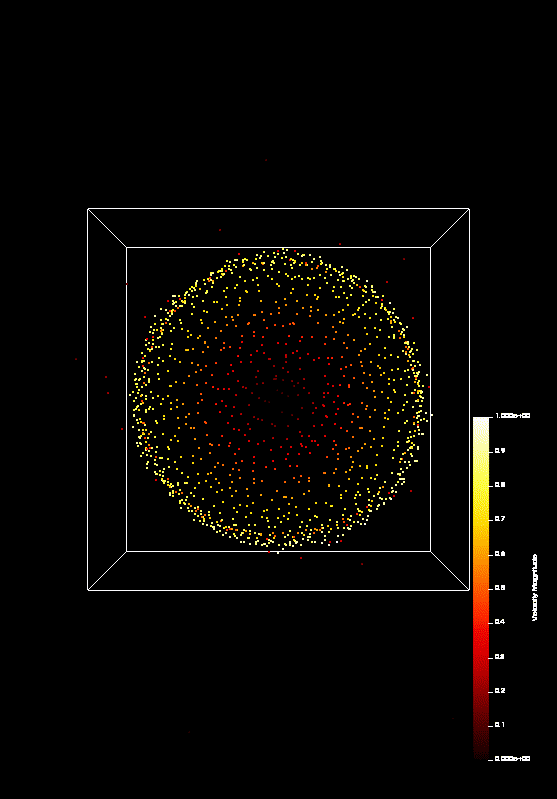
We predict that Coulomb explosion of a nanoscale cluster, which is ionized by high-intensity laser radiation and has a naturally occurring spatial density profile, will invariably produce shock waves. In most typical situations, two shocks, a leading and a trailing one, form a shock shell that eventually encompasses the entire cluster. Being the first example of shock waves on the nanometer scale, this phenomenon promises interesting effects and applications, including high-rate nuclear reactions inside each individual cluster.

But how to simulate it? With Newtonian Mechanics, which yields the following set of equations:

\[\ddot{x}_i = a_i = \sum_{j != i} a_{i,j}\]

\[a_{i,j}=\frac{q_iq_j}{\sqrt{(x_i-x_j)(x_i-x_j)}^3}(x_i-x_j)\]

Velocity Verlet integration:

\[v^*(t+ \frac{\Delta t}{2})=v(t) + \frac{\Delta}{2}a(t)\]

\[x(t+\Delta t) = x(t) + v^*(t+\frac{\Delta t}{2})\Delta t\]

\[v(t+\Delta t) = v^*(t+\frac{\Delta t}{2})+\frac{\Delta t}{2}a(t+\Delta t)\]

To wrap it up in words: every particle \(i\) is influenced by any other particle \(j\) and therefore, every contribution \(j\) on \(i\) needs to be calculated. All of these contributions can be computed independtly, thus making a parallelization of it quite easy. Suppose you have some structure or class in C++, that takes care of the following pseudo algorithm:

get initial state
compute accelrations
for number of time steps:
        calculate helper velocities v*
        calculate new positions x
        calculate new accelerations a
        calculate new velocities v

As previously mentioned within the time loop, at the point where the accelerations are computed, a team of threads can kick in and compute every contribution in parallel instead of a serial, tedious computation.

Take the following code snippet, for example:

void accelerations_calculate_self(
    std::size_t np,
    double ax[],
    double ay[],
    double az[],
    const double x[],
    const double y[],
    const double z[],
    const double q[]
) {
  for (std::size_t i = 0; i < np; ++i) {
    double accx = 0.0;
    double accy = 0.0;
    double accz = 0.0;

    for (std::size_t j = 0; j < i; ++j) {
      double dx = x[i] - x[j];
      double dy = y[i] - y[j];
      double dz = z[i] - z[j];
      double r = std::sqrt(dx * dx + dy * dy + dz * dz);
      double acc = q[i] * q[j] / (r * r * r);

      accx += acc * dx; accy += acc * dy; accz += acc * dz;
    }

    for (std::size_t j = i + 1; j < np; ++j) {
      double dx = x[i] - x[j];
      double dy = y[i] - y[j];
      double dz = z[i] - z[j];
      double r = std::sqrt(dx * dx + dy * dy + dz * dz);
      double acc = q[i] * q[j] / (r * r * r);

      accx += acc * dx; accy += acc * dy; accz += acc * dz;
    }

    ax[i] += accx; ay[i] += accy; az[i] += accz;
  }
}

The first loop takes care to loop over all particles \(i\), whereas the second and third loop covers the summation over \(j\). The loop over \(j\) is split, due to the fact, that you want o avoid, that a contribution of \(i\) onto \(i\) is calculated. Anyways, with one additional line of code, you can get a speedup of >20. Namely, by including one, single OpenMP pragma.

#pragma omp parallel for

right before the first for loop and you're done. Beautiful stuff.