My PhD in a Nutshell Part I: Motivation

In this post I'll introduce one open research question in computational mechanics as well as one research direction that tries to resolve the problem. All figures are produced by a small Julia code that resides inside a Pluto.jl notebook. The link to the notebook file can be found here or at the very bottom of this post.

My PhD Topic is a research project of the Chair of Mechanics - Continuum Mechanics, Ruhr-University Bochum in collaboration with Institute of Mathematics, University of Augsburg under the hood of the SPP 2256. The name of the project is Convexified Variational Formulations at Finite Strains based on Homogenised Damaged Microstructures. While this sounds incredibly hard to understand, the basic idea behind is quite simple and straightforward to explain. In order to do so, the point of departure needs to be clarified first.

When dealing with continuum damage mechanics, you probably stumble across a prominent scheme, called $(1-D)$. This scheme dates back to Karachnov,1958 and can be considered as one of the most basic, yet phenomenological sound damage models. Within this model, there exists a local variable $D$ that lives in the material point and describes how much of the material is damaged. Thus, $(1-D)$ leads to an expression of remaining effective quantity. If we consider some strain energy density function that stores the density of strain energy within a physical body, we can redefine it such that incorporates a damaging behavior by

\[ \psi(\boldsymbol{F}^T\boldsymbol{F},D(\beta)) \coloneqq (1-D(\beta))\psi^0(\boldsymbol{F}^T\boldsymbol{F}). \]

Here, $\psi^0$ is called effective strain energy density and it is a virtually undamaged strain energy that models the underyling material. In the Ferrite.jl docs there is a hyperelasticity example that shows how to define data structures and functions for strain energy densities. We take the Neo-Hooke example from there as an exemplary $\psi^0$:

Base.@kwdef struct NeoHooke
    μ::Float64 = 0.5
    λ::Float64 = 0.0
end

function Ψ(C::T, mp::NeoHooke) where T <: AbstractTensor{2,1}
    μ = mp.μ
    λ = mp.λ
    Ic = tr(C) + 2
    J = sqrt(det(C))
    return μ / 2 * (Ic - 3) - μ * log(J) + λ / 2 * log(J)^2
end

Note that I changed the normalization (property that describes for which argument $\psi^0$ is equal to 0) for the special case of having a purely one-dimensional deformation measure. We will restrict ourselves to one-dimensional computations in this post and thus, don't require multidimensional formulations. Since we have one underlying $\psi^0$ at hand, we can focus again on the damage variable $D$. The damage variable $D$ is not itself the internal variable, but rather $\beta$, which is defined as

\[ \beta \coloneqq \max_s [\psi^0(s)] \qquad s\in [0,t]. \]

This definition of $\beta$ models discontinuous damage and can be considered as standard. Rigorous derivation and analysis was done in Miehe,1995 (unfortunately no paper online, write me if you need it). Discontinuous damage refers to the modeling of damaging behavior only if new peak loads (primary loads) are reached within the material point. In contrast, continuous damage formulates a continuous growth of damage even if the current load is not a primary loading. The materials of our interest behave like discontinuous damage and therefore, we focus on this formulation. Within the aforementioned publication examples for damage functions are given that map the internal variable to the actual damage value

\[ D(\beta) = D_{\infty} \left[1-\exp\left(\frac{-\beta}{D_0}\right)\right]. \]

Here, $D_{\infty} \in (0,1)$ and $D_0$ are material dependent parameters. Defining this function in Julia is straightforward, you can defined it as you would do with any other function:

function damage_exponential(β; D∞=0.99, D₀=0.5)
    D∞ * (1 - exp(-(β / D₀)))
end

Below you can see a plot of the function for $D_{\infty} = 0.99$ and $D_{0} = 0.5$. From the plot we can conduct that $D_{\infty}$ controls the asymptotic value, whereas $D_{0}$ controls the initial slope, i.e. how fast $D_{\infty}$ is attained.

Later, we want to make use of the principle of minimum of potential energy. Thus, a potential formulation is required. Damage is a dissipative (history dependent, energy releasing) process that we want to include. A mathematical framework to derive such formulations is the incremental variational formulation framework. This conceptual idea takes a dissipative process and formulates thermodynamic consistent per incremental step pseudo-elastic potentials. Pseudo-elastic refers here to the fact that each incremental variational formulation depends solely on a deformation (or strain) measure. The basic ingredients of the framework are to describe a strain energy density $\psi$ (completed) and a dissipation potential $\phi$ that form together the generalized energy $\mathcal{W}$. The dissipation potential $\phi$ can be obtained when evaluating the reduced Clausius-Duhem inequality and results in

\[ \phi \coloneqq \psi^0 \dot{D} = \beta \frac{\partial D}{\partial \beta} \dot{\beta} > 0. \]

Since we have all ingredients at hand, we can derive now the incremental variational formulation by

\[ W(\boldsymbol{F}_{k+1}) = \inf_{\beta_{k+1}}[\mathcal{W}(\boldsymbol{F}_{k+1}, \beta_{k+1})] \quad \text{with} \quad \mathcal{W}(\boldsymbol{F}_{k+1}, \beta_{k+1}) \coloneqq \int_{t_k}^{t_{k+1}} \dot{\psi} + \phi \ dt. \]

Note that after minimizing the generalized energy $\mathcal{W}$, the incremental stress potential (also called reduced or condensed energy) has only a dependency w.r.t. $F$. Reduced or condensed is actually a very nice description of the process. What we just did is a pointwise minimization w.r.t. $\beta$ and therefore, we "condensated" the variable out of the problem. Luckily, the minimization w.r.t. the internal variable $\beta$ can be done analytically, which is presented in Balzani and Ortiz, 2012. Analytic minimization yields the following formula for the incremental stress potential

\[ W(\boldsymbol{F}) = \psi(\boldsymbol{F}, D) - \psi(\boldsymbol{F}_{k},D_{k})+\beta D - \beta_{k} D_{k} - \tilde{D} + \tilde{D}_{k} \]

where $(\cdot)$ is the current incremental step (so, $k+1$), $(\cdot)_{k}$ the previous and, $\tilde{D}$ denotes the anti-derivative of the damage function. One Julia realization of this description could be:

Base.@kwdef struct UnrelaxedDamage
    base_material::NeoHooke = NeoHooke()
    D₀::Float64 = 0.5
    D∞::Float64 = 0.99
end

Base.@kwdef struct UnrelaxedDamageState
    βₖ::Float64 = 0.0
    ψₖ::Float64 = 0.0
end

function W(F,material,state)
    ψ₀ = Ψ(tdot(F), material.base_material)
    β = max(ψ₀, state.βₖ)
    D = damage_exponential(β;D∞=material.D∞, D₀=material.D₀)
    Dₖ = damage_exponential(state.βₖ;D∞=material.D∞, D₀=material.D₀)
    D_anti = damage_exponential_antiderivative(β;D∞=material.D∞, D₀=material.D₀)
    D_antiₖ = damage_exponential_antiderivative(state.βₖ;D∞=material.D∞, D₀=material.D₀)
    ψ = (1 - D) * ψ₀
    ψₖ = (1 - Dₖ) * state.ψₖ
    W = ψ - ψₖ + β * D - state.βₖ * Dₖ - D_anti + D_antiₖ
    return W
end

Given a fixed $\beta$ we can plot the function $W(F)$ with its dependency to the deformation measure $F$.

From the plot it is obvious that we have a non-convex formulation. Mechanically, this is a sound feature, because if you travel along the function and take successively the derivative, which corresponds to a certain stress measure, you get all effects you want to model.

At this point, we can introduce the following abbreviations:

\[ \boldsymbol{P} = \frac{\partial W(\boldsymbol{F})}{\partial \boldsymbol{F}} \qquad \text{and} \qquad \mathbb{A} = \frac{\partial^2 W(\boldsymbol{F})}{\partial \boldsymbol{F}^2}, \]

where $\boldsymbol{P}$ denotes the first Piola-Kirchhoff stresses (nominal stresses) and $\mathbb{A}$ the nominal tangent moduli.

In the plot above the stresses over the deformation gradient $F$ are plotted. The plot was created by calling the following constitutive_driver (material law) implementation for different prescribed deformation gradients:

function constitutive_driver(F, material::UnrelaxedDamage, state::UnrelaxedDamageState)
    𝔸, P = Tensors.hessian(y -> W(y, material, state), F, :all)
    ψ = Ψ(tdot(F), material.base_material)
    β = max(state.βₖ, ψ)
    newstate = UnrelaxedDamageState(β,ψ)
    return P, 𝔸, newstate
end

The desirable behavior of decreasing stress with increasing deformation is called strain-softening and one of the key features to describe by damage models. While it is easy to find sound mechanical formulations that model this, it is mathematically problematic to describe strain softening by non-convexity.

If we consider the problem we would like to solve, i.e. finding the minimum of a potential

\[ \Pi = \int_{\mathcal{B}} W(\boldsymbol{F}) \ dV - \Pi^{\text{ext}} \rightarrow \text{stationary}, \]

where we discretize the body $\mathcal{B}$ with finite elements, take the Gateaux derivative and set it equal to zero

\[ \delta \Pi = \int_{\mathcal{B}} \delta \boldsymbol{F} \cdot \partial_{\boldsymbol{F}} W(\boldsymbol{F}) \ dV - \Pi^{\text{ext}} = 0, \]

we obtain an ill-posed problem as soon as we enter the non-convex regime of $W(F)$. The direct method of the calculus of variations tells us that if $W(F)$ is weakly lower semicontinuous, coercive and bounded from below then $W(F)$ has minimizers. However, it doesn't make any statements about the uniqueness of the minimizer. In order to provide uniqueness we need convexity (more details in e.g., Bartels, 2015, section 2.2), but what does this imply to our finite element discretization of the problem if the potential density (the integrand) is non-convex?

To find the minimum of the potential energy, we utilize a Newton scheme with the following residual

\[ \mathcal{F}(\boldsymbol{u}) = \int_{\mathcal{B}} \nabla_X \delta \boldsymbol{u} : \boldsymbol{P} \ dV = 0, \]

and the Jacobian

\[ \frac{\partial \mathcal{F}(\boldsymbol{u})}{\partial \boldsymbol{u}}=J(\boldsymbol{u}) = \int_{\mathcal{B}} \nabla_X \delta \boldsymbol{u} : \mathbb{A} : \nabla_X \delta \boldsymbol{u}. \]

If you need some good introductory writings about the Newton's method within the variational setting or numerical methods for variational methods in general, I highly recommend Langtangen & Mardal,2019. Take a look at section 9.1.8 if you need some additional information about Newton's method. Note that I ignored in the derivation above any external forces and thus Neumann boundary conditions as well as the body forces (both equal to zero in our example case of this post). You can see how to incorporate them within the hyperelasticity example of Ferrite.jl. We will see now how the non-convexity effects the finite element discretization. For this we consider an imperfect bar with two linear, one-dimensional elements and parametrize their length by a parameter $\kappa$. The total length, however, is kept fixed to $L$.

The second element gets a small numerical distortion $\epsilon=10^{-8}$ for the $D_\infty$ parameter. Note that the distortion is extremely small and therefore has no physical relevance. The boundary conditions of the problem are the following: The left-hand side node, filled in white, gets a homogeneous Dirichlet boundary condition assigned, whereas the right-hand side node, filled in red, is pulled by a linearly increasing Dirichlet boundary condition. Thus, the only true degree of freedom is the middle node, marked in blue. I discretized the problem for $\kappa \in \{0.3,0.5,0.7,1.0\}$. Below you can see the force-displacement plots for the different discretizations. The tealer the curve, the higher is the chosen $\kappa$ value.

It is quite surprising to see completely different plots, even though the distortion is very small. This phenomena is called mesh-dependence or mesh-sensitivity and should not be confused with the mesh dependence w.r.t. the approximation quality. The classical mesh dependence in terms of the approximation quality is known to vanish for sufficiently fine meshes (higher order Ansatzes, respectively). However, if you refine the mesh all you get is softener responses. A more mechanical reasoning about this phenomenon can be found in de Borst et. Al, 2012,section 6.4 or Murakami,2012,chapter 11 What we observe here is the loss of ellipticity of the governing partial differential equation, which is directly connected to properties of $W(F)$. Since we restrict ourselves to the one-dimensional case in this post, we can require that $W(F)$ is convex in order to avoid the loss of ellipticity. The loss of ellipticity can directly be connected to a certain (semi)convex notion. However those notions coincide in the one-dimensional case and reduce to convexity. The basic idea about the research direction I'm part of, is, to replace the non-convex $W(F)$ and substitute it by the largest convex function below it, which is the convex hull of the function. In order to do so, we need to clarify what convexity means mathematically.

A function $W:\R\to\R$ is said to be convex if \( W(\xi F^+ + (1-\xi)F^-) \leq \xi W(F^+) + (1-\xi) W(F^-) \) holds for all $\xi \in (0,1)$ and $F^+, F^- \in \R$. Alternatively, a function is convex if its first derivative is monotonically increasing. By that the convexity condition can be reformulated as \( \left(W'(F^+) - W'(F^-)\right)(F^+ - F^-) \geq 0, \) which will be utilized later.

If the function $W(F)$ is not convex, we can obtain its convex envelope (hull) $W_C(F)$ by finding the two supporting points of the convex hull. The supporting points of the convex hull $F^+$ and $F^-$ parameterize the deformation gradient $F$ along with the volume fraction $\xi$ \( F\coloneqq \xi F^+ + (1-\xi)F^- , \) based thereon, we can reformulate $F^+$ and $F^-$ \( F^+ \coloneqq F(1+(1-\xi)d) \qquad \text{and} \qquad F^- \coloneqq F(1-\xi d) \) w.r.t. $\xi$ and $d$, such that we end up with the following two-dimensional highly multimodal optimization problem

\[ W \leftarrow W_C(F) = \inf_{\xi,d} [\overline{W}(F,d,\xi)] \qquad \text{with} \qquad \overline{W} = \xi W(F^+) + (1-\xi) W(F^-) \]

If we replace the non-convex formulation $W(F)$ within our finite element discretization by the convex hull $W_C(F)$ all we need to change is the constitutive response. This is due to the fact that only $\boldsymbol{P}$ and $\mathbb{A}$ require the incremental stress potential (since they are simply the first and second derivative thereof). This procedure is called relaxation, since you relaxe or ease the problem. From a minimization perspective, we'd like to find the minimum of potential energy. Thus, a multimodal function is harder to minimize than a unimodal one. Nice properties of relaxation within the variational setting are that it does not require additional field variables with length scale parameters, which is a more prominent research direction that tries to find an answer to the computational problem of strain-softening behavior. The more interesting property of relaxation is that the supporting points of the convex hull $F^+$ and $F^-$ form a very interesting mathematical object. These points are minimizers to the original problem and the convex hull can be expressed in the convexified regime as the convex combination \( \xi W(F^+) + (1-\xi) W(F^-). \) This convex combination expresses a mixture of two deformation states that correspond to quasi homogenized solutions. But more about that (maybe) in a later post. In order to apply relaxation to our problem, the main question is: How can we construct the convex hull efficiently? The previously introduced non-linear multimodal global optimization problem is hard to solve and we would like to replace it by something that is computationally cheaper. It is one of the main questions I'd like to answer within my PhD and we investigated one way in the one-dimensional setting that turns out to be quite fast. The idea is to apply a variation of the Graham Scan. Applying such an algorithm in a variational setting was written down in Bartels, 2015, below Algorithm 9.3. A pseudocode can be written in the following way:

initialize function values f and a copy g based on discretization x
for j >= 1 to length(x) do
    if (g[j] - g[j-1])/(x[j] - x[j-1]) < (g[j-1] - g[j-2])/(x[j-1] - x[j-2]) then
        find smallest 0 < k < j-1, s.t.
        (g[j] - g[j-1])/(x[j] - x[j-1]) >= (g[j-1] - g[j-2])/(x[j-1] - x[j-2]) 
        for m = 1 to k do
            succesive linear Taylor expansion
            g[j-m] = g[j-k] + (x[j-m] - x[j-k]) * ((g[j] - g[j-k])/(x[j] - x[j-k]))
        end for
    end if
end for

This procedure scans from left to right the monotonicity property of the finite differences derivative of the function values f. If the condition is violated, the point were the condition held true for the last time is sought. A visualization of the algorithm is depicted below:

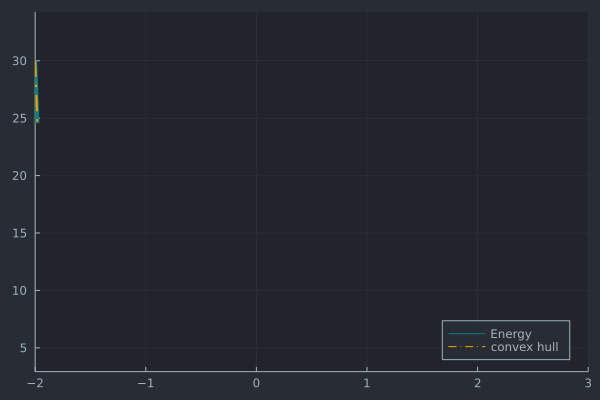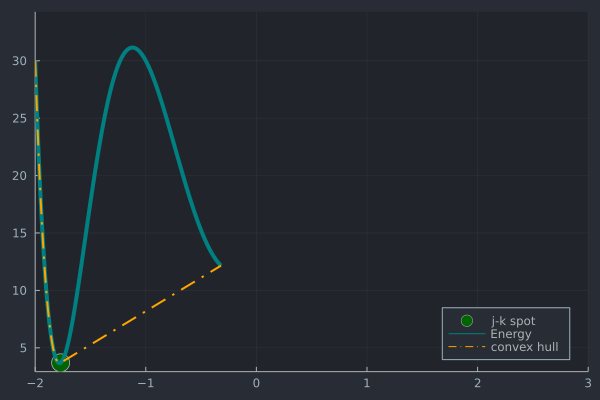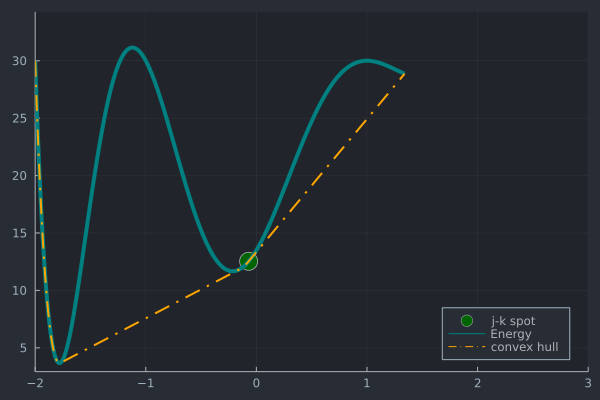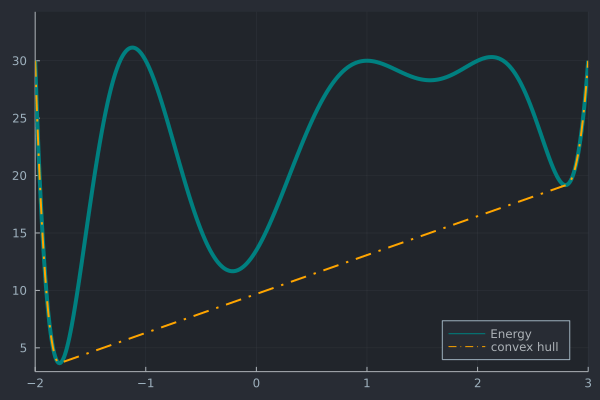
We can implement this in Julia by e.g.

function convexify!(F,material,state) 
	grid = copy(material.deformation_grid)
    grid_F = [Tensor{2,1}([x]) for x in material.deformation_grid]
    𝐠 = [W(x, material, state) for x in grid_F]
    j = 3
    i = 3
    l = length(𝐠)
    while j < length(𝐠) - 1 && i < l        
        if (𝐠[j]-𝐠[j-1])/(grid[j]-grid[j-1]) < (𝐠[j-1]-𝐠[j-2])/(grid[j-1]-grid[j-2])
            true_k = j - 1
            for k in 1:(j-2)
                if (𝐠[j]-𝐠[j-k])/(grid[j]-grid[j-k]) >= (𝐠[j-k] - 𝐠[j-k-1])/(grid[j-k]-grid[j-k-1])
                    true_k = k
                    break
                end
            end
            deleteat!(grid, j-true_k+1:j-1)
            deleteat!(𝐠, j-true_k+1:j-1)
            j += - true_k + 1    
        end
        j += 1
        i += 1 
    end
 
	plus_idx =  findfirst(x -> x >= F[1], grid)
	minus_idx = findlast(x -> x <= F[1], grid)
	F⁺ = grid[plus_idx]
	F⁻ = grid[minus_idx]
	if 𝐠[minus_idx] + (F[1] - grid[minus_idx]) *((𝐠[plus_idx] - 𝐠[minus_idx])/(F⁺ - F⁻)) < W(F,material,state)
		convex = false
	else
		convex = true
	end
	return convex, Tensor{2,1}([F⁺]), Tensor{2,1}([F⁻])
end

Note that this implementation is far from optimal. While we gain linear complexity by deleting all points that are above the convex hull, we spend a lot of time deleting actual memory. A more sophisticated implementation can circumvent this and by that, a lot of overhead with copying arrays is saved.

Now, we can incorporate this function into our new material routine. In order to provide a new dispatch, we also need to introduce a new material and state struct.

Base.@kwdef struct RelaxedDamage
	base_material::NeoHooke = NeoHooke()
	deformation_grid::Vector{Float64} = collect(1.0:0.005:16)
	D₀::Float64 = 0.5
	D∞::Float64 = 0.99
end

Base.@kwdef struct RelaxedDamageState{dim,T,N}
	convex::Bool = true
	βₖ::Float64 = 0.0
	ψₖ::Float64 = 0.0
	F⁺::Tensor{2,dim,T,N} = Tensor{2,1}((1.0,))
	F⁻::Tensor{2,dim,T,N} = Tensor{2,1}((1.0,))
end

init_materialstate(mat::RelaxedDamage) = RelaxedDamageState()

function Wᶜ(F,ξ,d,material,state)
	F⁺ = F * (1 + (1 - ξ) * d)
    F¯ = F * (1 - ξ * d)
    W⁺ = W(F⁺, material, state)
    W¯ = W(F¯, material, state)
    return ξ * W⁺ + (1 - ξ) * W¯
end

function constitutive_driver(F, material::RelaxedDamage, state::RelaxedDamageState)
	F⁺ = state.F⁺
	F⁻ = state.F⁻
	convex = state.convex
	if convex
		convex,F⁺,F⁻ = convexify!(F,material,state)
	end
	if convex
		𝔸, P = Tensors.hessian(y -> W(y, material, state), F, :all)
	    ψ = Ψ(tdot(F), material.base_material)
	    β = max(state.βₖ, ψ)
	    newstate = RelaxedDamageState(convex,β,ψ,F⁺,F⁻) 
	else
		ξ = (F[1] - F⁻[1]) / (F⁺[1] - F⁻[1])
		d = (F⁺[1] - F⁻[1]) / F[1]
		𝔸, P, Wc = Tensors.hessian(y -> Wᶜ(y, ξ, d, material, state),F,:all)
		newstate = RelaxedDamageState(convex,state.βₖ,state.ψₖ,F⁺,F⁻)
		#if we exceed the convexified regime; need a way out of the !convex branch
		if Wc >= W(F,material,state) || isapprox(Wc,W(F,material,state))
			𝔸, P = Tensors.hessian(y -> W(y, material, state), F, :all)
	    	ψ = Ψ(tdot(F), material.base_material)
	    	β = max(state.βₖ, ψ)
			convex = true
			newstate = RelaxedDamageState(convex,β,ψ,F⁺,F⁻) 
		end
	end
    return P, 𝔸, newstate
end

Now, we are set to test again the imperfect bar for different $\kappa$s. I tested the new material routine against the very same setups as before. The force-displacement plot below show the new relaxed formulation as solid orange line for all $\kappa$s. The curves coincide and the loss of ellipticity and thus the instability was circumvented.

However, the softening behavior is gone. One might ask, what's it worth of spending so much time in a one-dimensional model if it can't even model strain softening? Well, we just arrived at the second big topic of my PhD: How can we incorporate softening behavior when using relaxed formulations? The convex hull has clearly a constant derivative in the convexified regime and thus the stresses (first derivative) are constant whenever relaxation is applied. Nonetheless, I have some nice ideas how to get the softening behavior back, while still providing mesh-independent solutions. More about that later.

## The notebook file with all the code to reproduce the figures